MATLABで設計した状態フィードバック制御器をUnityで実装&動かしてみる
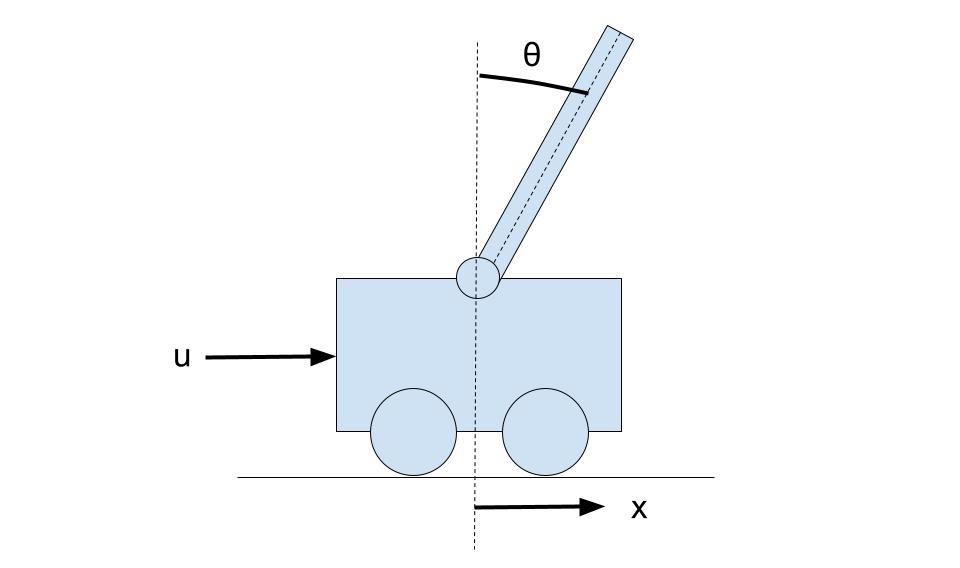
前回までMATLABで以下の台車型倒立振子の状態フィードバック制御器を設計して、MATLABで初期状態の応答をシミュレーションしてみたり、Simulinkで外部入力を加えた時の応答をシミュレーションしてみた。
ただ、波形を見てるだけだとちょっと味気ない。ということで、今回はUnityで台車型倒立振子のモデルをつくり、MATLABで設計した制御器を実装してアニメーションで動作を確認してみたので、その方法をメモしておく。
誤解が無いように書いておくと、今回のやり方はMATLABとUnityを通信させて制御しているわけではなく、MATLAB上で計算したフィードバックゲインKを使って、C#で実装したコードをUnity上で動かす、という感じ。
台車型倒立振子のモデリングやMATLABでの状態フィードバック制御器の設計については以下を参照。
開発環境
MATLAB online(MATLAB R2022a)
Simulink
Control System Toolbox
Unity 2021.3.7f1
Windows 10
MATLABで状態フィードバックのゲインを計算
こちらは以前のおさらいなので詳細は割愛するが、以下のmファイルMATLABを実行して、以前定義した各状態変数x、dx/dt、θ、dθ/dtに対する状態フィードバック制御のゲインKを計算しておく。
% Parameters
M = 10;
m = 1;
L = 2;
g = 9.8;
% State Space
A = [0 1 0 0
0 0 -3*m*g/(4*M+m) 0
0 0 0 1
0 0 6*g*(M+m)/(L*(4*M+m)) 0];
B = [0
4/(4*M+m)
0
-6/(L*(4*M+m))];
% Check Controllability
Co = ctrb(A,B);
rank(Co)
% Pole/Feedback Gain
p = [-0.5 -1.0 -1.5 -2.0];
K = place(A,B,p)
これを実行すると、以下のようなフィードバックゲインKが得られた。
K = -2.0918 -8.716 -230.1724 -79.9546
実際に実機を作って動かす場合には各状態変数x、dx/dt、θ、dθ/dtを全てセンサーで測定するのは現実的ではないが、Unityであればオブジェクト(台車や振子のモデル)に付加したrigidbodyから各状態変数の値を取得できる。
そのため、ここで計算したゲインKを、Unity上で取得した各状態変数x、dx/dt、θ、dθ/dtにかけて足し合わせた入力uを台車に加えれば、状態フィードバック制御のシミュレーションができる。
Unityで台車型倒立振子をモデリング
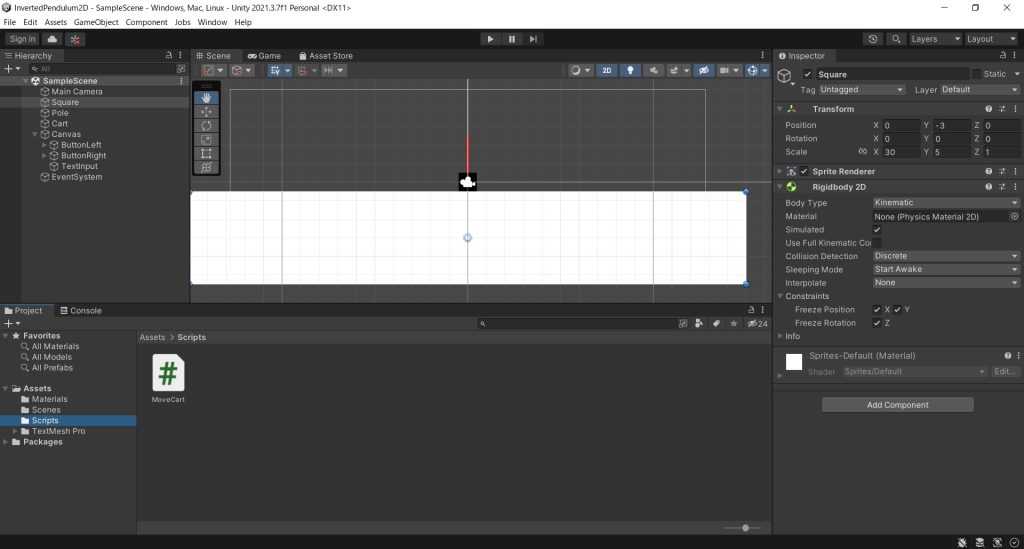
まずは台車のモデリングから。Unityは最新のLTS版であるUnity 2021.3.7f1を使用した。今回は2Dでプロジェクトを作成した。あまり細かく説明しないが、Inspectorの設定だけ張っておくのでやりたい人は参考にしてください。まず、床は2D Object→Sprites→Squareで配置してRigidbodyを追加。
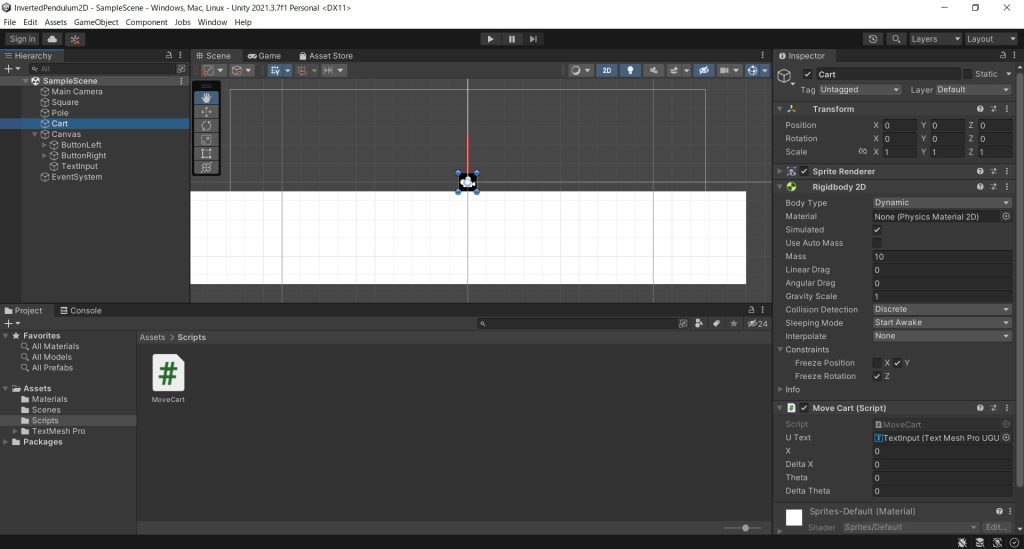
次に台車を、先ほどと同じくSquareでCartという名前で配置してRigidbodyを付加した。台車のタイヤは無くても摩擦を0に設定すればOKなので割愛。質量(Mass)はMATLABの計算で使った値と合わせている。
振子の棒もSquareでPoleという名前で配置して、Rigidbody&Hinge Joint 2Dで台車と接続した。こちらも寸法や質量(Mass)はMATLABの計算で使った値と合わせている。
ButtonとTextも配置しているが、こちらは次の節で書く。
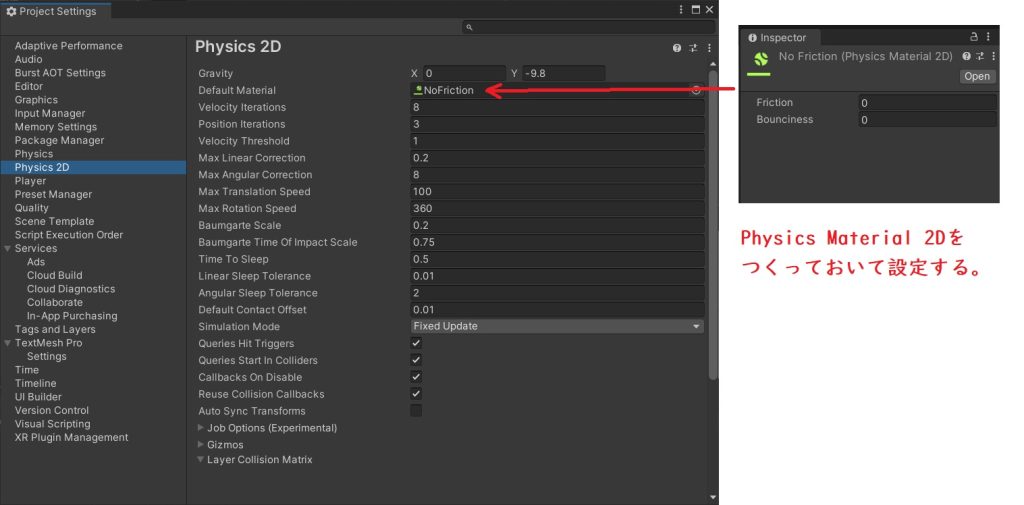
また、Edit→Project SettingsからPhysic 2Dの設定を開き、重力加速度を-9.8(デフォルトは-9.81だが、MATLABで計算したときの値に合わせた)、摩擦を0にしたphysics materialをDefault Materialに設定して、MATLABでのモデルにパラメータが合うようにした。
台車を動かす制御器をC#で実装する
オブジェクトが配置できたら、Cartに以下のようにMoveCart.csというスクリプトを追加した。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using TMPro;
public class MoveCart : MonoBehaviour
{
private GameObject refObj;
private float x;
private float deltaX;
private float theta;
private float deltaTheta;
public TextMeshProUGUI uText;
private float k1 = -2.0918f;
private float k2 = -8.716f;
private float k3 = -230.1724f;
private float k4 = -79.9546f;
// Start is called before the first frame update
void Start()
{
refObj = GameObject.Find( "Pole" );
uText.text = "u = 0";
}
// Update is called once per frame
void FixedUpdate()
{
Rigidbody2D rb = this.GetComponent();
Vector2 force = new Vector2(0.0f, 0.0f);
x = rb.position.x;
deltaX = rb.velocity.x;
theta = refObj.GetComponent().rotation * Mathf.Deg2Rad;
deltaTheta = refObj.GetComponent().angularVelocity * Mathf.Deg2Rad;
float u = -k1 * x + -k2 * deltaX - k3 * (-theta) - k4 * (-deltaTheta);
uText.text = "u = " + u.ToString();
force = new Vector2(u, 0.0f);
rb.AddForce (force);
}
public void OnClickLeft() {
Rigidbody2D rb = this.GetComponent();
Vector2 force = new Vector2(0.0f, 0.0f);
force = new Vector2(300f, 0.0f);
rb.AddForce (force);
}
public void OnClickRight() {
Rigidbody2D rb = this.GetComponent();
Vector2 force = new Vector2(0.0f, 0.0f);
force = new Vector2(-300f, 0.0f);
rb.AddForce (force);
}
}
一点補足しておくと、
float u = -k1 * x + -k2 * deltaX - k3 * (-theta) - k4 * (-deltaTheta);
について、まずMATLABで求めたKはフィードバックするときの符号はマイナスになるのでk1~k4の符号はマイナスになる。加えて、振子の棒の角度θは、状態変数を求めた時に定義した方向と、Unityで定義されている方向で符号が逆になるため、thetaとdeltaThetaの符号をマイナスにしている。
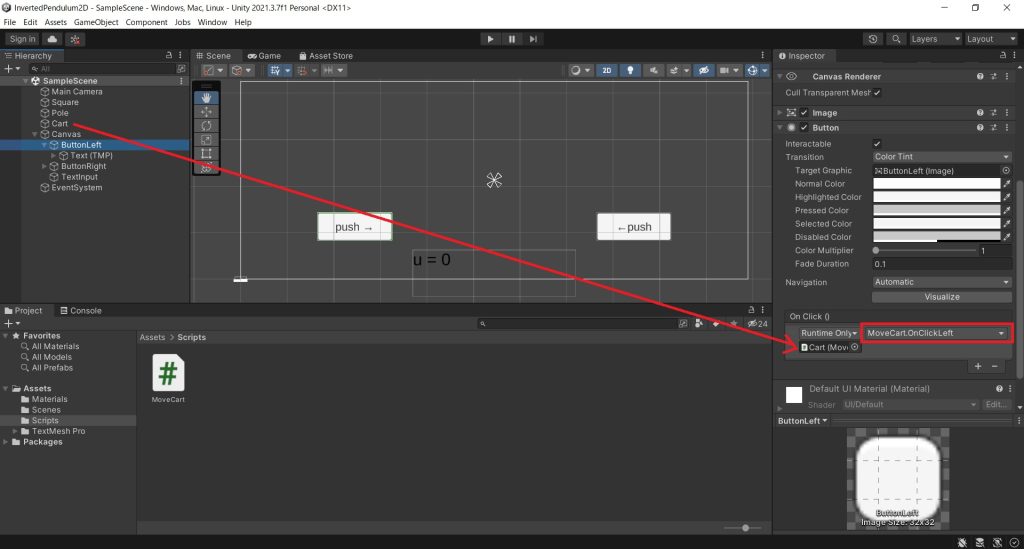
MATLABやSimulinkでやったような初期条件からの応答を見てもよかったのだが、せっかくなのでOnClickLeft/OnClickRightという関数を実装して、ボタンをクリックして台車を横から突っつけるような実装にした。ボタンはUIのButtonオブジェクトを追加し、追加したButtonの「Button」にMoveCart.csを付加したCartオブジェクトを設定し、ボタンをクリックした関数を実行できるようにした。
また、UIからTextも追加して、uText.text = “u = ” + u.ToString();でuの値を画面上に表示するようにした。ScriptからTextを変更する場合は、Publicで定義したMoveCartのuTextに、Textのオブジェクトを追加すればOK。
これで準備は完了。
実行して動かしてみる
後はUnityで動かすだけ。再生ボタンを押して、ボタンをクリックしてツンツンつついてみた様子が以下の動画。表示されているuの値が台車に加わり、倒立状態を維持できていることがわかる。
やはり動いている様子が見えると楽しい。前回の記事で書いたようにMATLAB OnlineだとMechanics Explorerでアニメーション表示ができないので、Unityを使うというのはなかなか良い気がする。今後も物理シミュレーターとしてUnityを活用していきたい。
参考文献
この本のMATLAB/Simulink 6か月ライセンスを使ってやってます↓
Interface 2022年 9月号
MATLAB/Simulink記事まとめ
MATLABとSimulinkの記事は以下にまとめてます。