MATLABで状態フィードバック制御器設計&シミュレーションをやってみる
私の中ではMATLABといえば制御!というイメージがあり、実際MATLABは行列計算を多用する現代制御理論ではかなり便利だと思う。ということで、今回から学生時代の記憶を掘り起こしながら、現代制御をテーマに色々と遊んでいこうと思う。
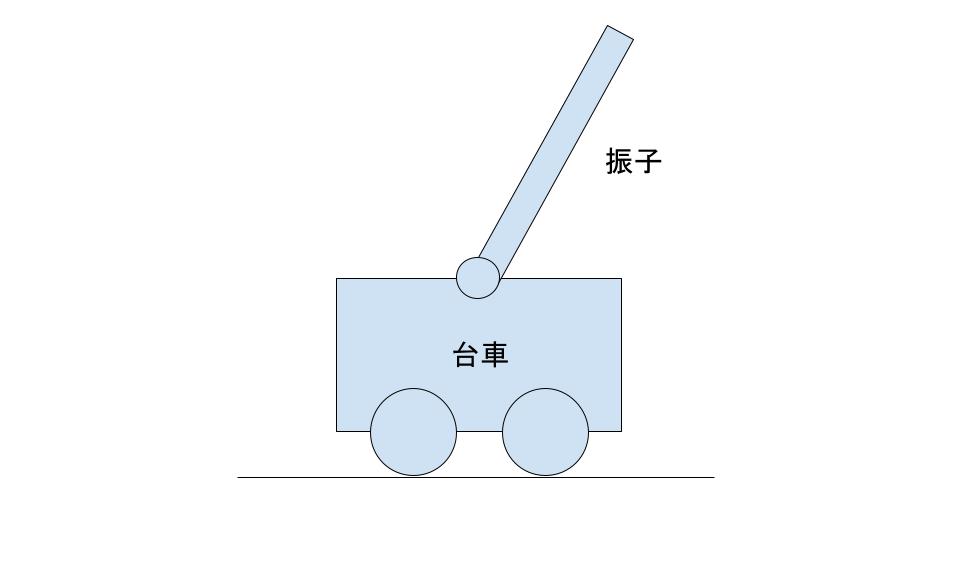
今回は題材として、教科書などでもよくでてくる台車型の倒立振子をテーマに、状態フィードバック制御をやってみたのでやり方をメモ。こういうやつ↓
ちなみに制御理論について細かい説明はしてないのであしからず。
開発環境
MATLAB online (MATLAB R2022a)
Simulink
Control System Toolbox
台車型倒立振子の状態方程式
まずは台車型倒立振子の状態方程式を求める必要があるのだが、一から求めるのは結構大変。ということで今回は先人の知恵を借りることにする。台車型倒立振子の状態方程式と一言でいっても状態変数や入力をどう定義するか?によって状態方程式も異なってくるのだが、今回は
- 状態変数:台車の変位(x)、速度(dx/dt)、振子の角度(θ)、角速度(dθ/dt)
- 入力:台車に加える力(u)
として、以下の線形化した台車型倒立振子のモデルをそのまま使わせて頂いたm(_ _)m
台車型倒立振子を安定にフィードバック制御する|Tajima Robotics
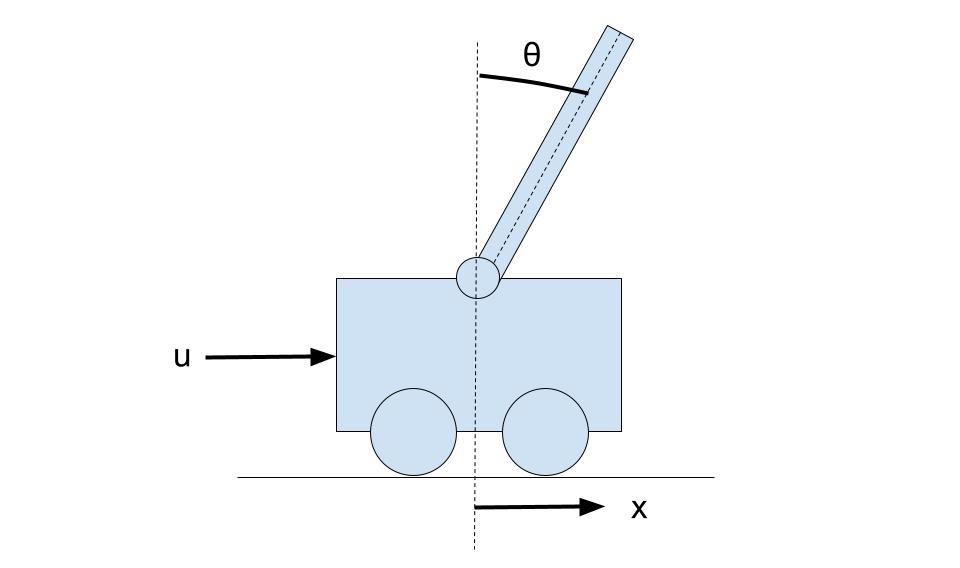
先ほどの絵に状態変数と入力を書き入れたのがこちら↓
台車の重さはM、振子の重さをm、振子の長さをl、振子の重心にかかる重力加速度はgとする。
MATLABで極配置&状態フィードバック制御器の設計&シミュレーション
今回は以下のようにMATLABでmファイルを実行してシミュレーションを実行した。
% Parameters
M = 10;
m = 1;
L = 2;
g = 9.8;
% State Space
A = [0 1 0 0
0 0 -3*m*g/(4*M+m) 0
0 0 0 1
0 0 6*g*(M+m)/(L*(4*M+m)) 0];
B = [0
4/(4*M+m)
0
-6/(L*(4*M+m))];
C = eye(4);
D = zeros(4,1);
% Check Controllability
Co = ctrb(A,B);
rank(Co)
% Pole/Feedback Gain
p = [-0.5 -1.0 -1.5 -2.0];
K = place(A,B,p);
% Simulation
x0 = [0;
0;
0.1;
0];
sys = ss(A-B*K,B,C,D);
initial(sys,x0);
ざっくり流れだけ書くと
- 各物理パラメータを定義
- 状態方程式で表したシステムを定義
- ctrb関数、rank関数で可制御性をチェック(Full Rankのため可制御なのでOK)
- 配置したい極の位置を決めて、place関数でフィードバックゲインKを計算
- 初期状態x0を定義し、ss関数で状態フィードバックをかけたシステムを定義してinitial関数で初期状態からの応答をSimulation
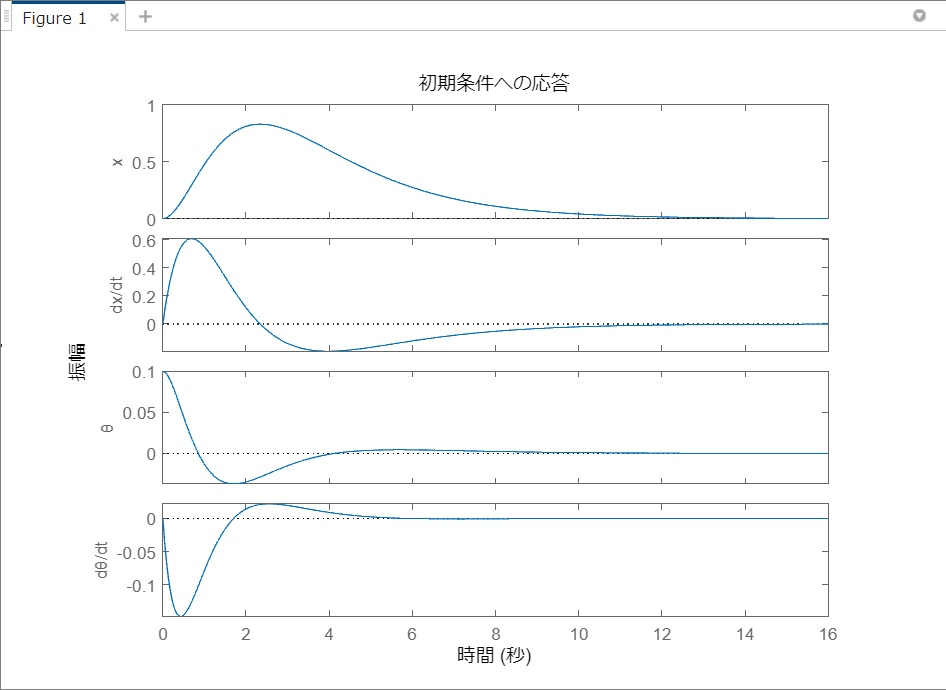
という感じ。initial関数を実行すると以下のように自動的にグラフが表示される(x軸のラベルは後から編集した)。以下はθが0.1[rad]傾いた状態からスタートさせた場合の応答だが、全ての状態変数が収束して安定化していることがわかる。
状態フィードバックをするには色々とややこしい計算が必要だが、MATLABの関数を使えばかなり簡単に計算できる。改めてMATLABって便利だな~と実感する。
今回はMATLAB上でシミュレーションまでやったが、次回はSimulinkでブロック図を使って同じシステムのシミュレーションをやってみたいと思う。
参考文献
この本のMATLAB/Simulink 6か月ライセンスを使ってやってます↓
Interface 2022年 9月号
現代制御理論の復習については以下を参考にさせて頂きましたm(_ _)m
MATLAB/Simulink記事まとめ
MATLABとSimulinkの記事は以下にまとめてます。