MATLABでサーボシステムを最適制御理論で設計&Unityで実装して動かしてみる
前回は台車型倒立振子の最適制御(最適レギュレータ)を設計して状態フィードバックをやってみたが、今回はサーボシステムの制御器を最適制御理論で設計してみる。制御対象は前回と同様に
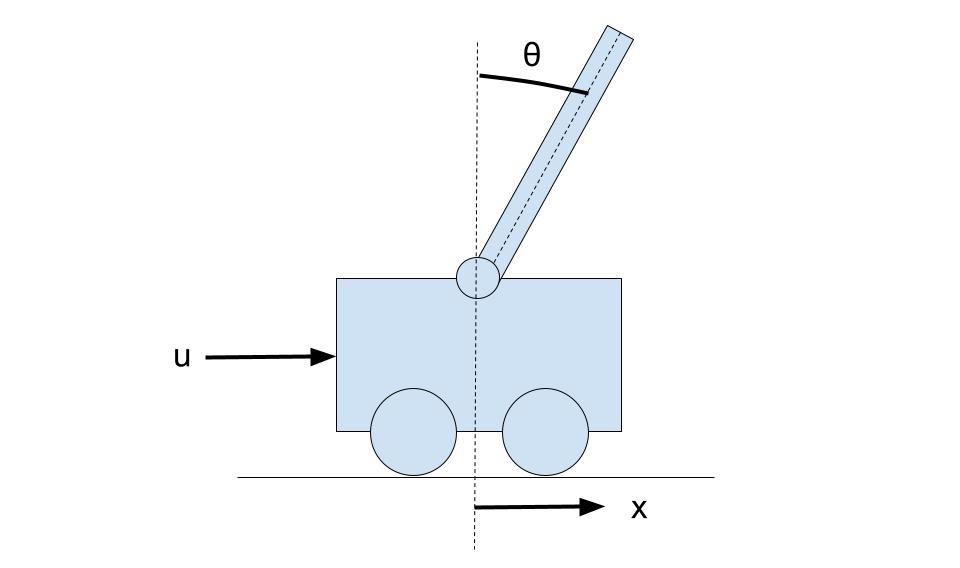
- 状態変数:台車の変位(x)、速度(dx/dt)、振子の角度(θ)、角速度(dθ/dt)
- 入力:台車に加える力(u)
として、以下の台車型倒立振子を対象とする。
なお、サーボ系の最適制御については目標値をフィードフォワードする形のものもあり、フィードフォワードした方が速応性の向上などが見込めるようだが、今回は簡単化のためにフィードフォワードは無しとした。
開発環境
MATLAB online (MATLAB R2022a)
Simulink
Control System Toolbox
Unity 2021.3.7f1
Windows 10
MATLABでサーボシステムのゲインを求める
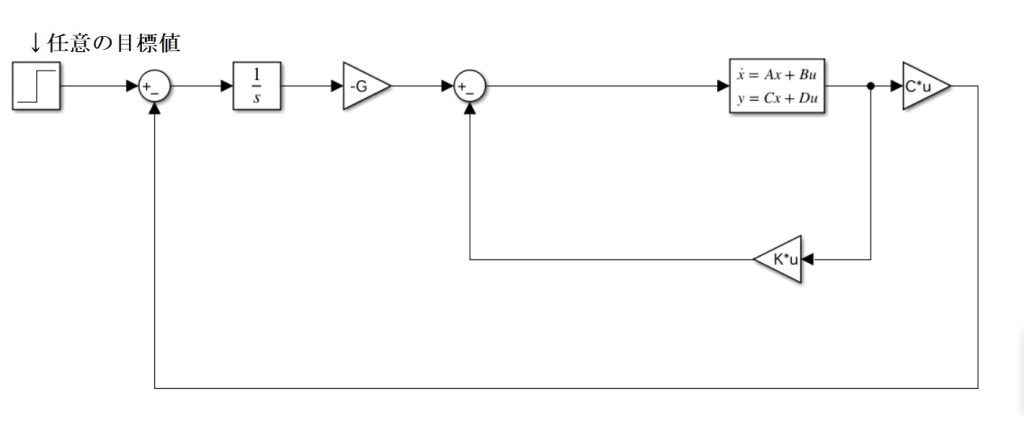
サーボシステムは、以前サーボシステムを設計したときと同様に以下の図のようなシステムとする。状態変数は、台車の変位(x)、速度(dx/dt)、振子の角度(θ)、角速度(dθ/dt)で、入力:台車に加える力(u)になっており、変位xを目標値に追従させるようなサーボシステムになっている。
このサーボシステムの制御器を最適制御理論で設計するために、目標値と出力yの偏差を状態変数に加えてA、Bを拡張し、Ae、Beとして以下のようにMATLABでmファイルを実行して、ゲインKとGを求めた。QとRは適当に決定した。
% Parameters
M = 10;
m = 1;
L = 2;
g = 9.8;
% State Space
A = [0 1 0 0
0 0 -3*m*g/(4*M+m) 0
0 0 0 1
0 0 6*g*(M+m)/(L*(4*M+m)) 0];
B = [0
4/(4*M+m)
0
-6/(L*(4*M+m))];
C = [1 0 0 0];
D = zeros(4,1);
Ae = [A zeros(4,1)
-C zeros(1,1)];
Be = [B
zeros(1,1)];
% Check Controllability
Co = ctrb(Ae,Be);
rank(Co)
%Linear Quadratic Regulator
Q = diag([30 30 100 50 30]);
R = 1;
Ke = lqr(Ae,Be,Q,R);
K = Ke(1,1:4)
G = Ke(1,5)
Matlabで計算したフィードバックゲインK、Gは以下の通り。
K = -19.4809 -31.9053 -396.7040 -143.7165 G = 5.4772
このゲインを使って、Unity上でC#のスクリプトを実装し、台車型倒立振子を目標値に追従させる。
Unityで台車型倒立振子の動作をシミュレーションしてみる
以前Unityでサーボシステムを動かしたときから変更する点は、MoveCartServo.csのソースコードのゲインを
private float k1 = -19.4809f;
private float k2 = -31.9053f;
private float k3 = -396.7040f;
private float k4 = -143.7165f;
private float g = 5.4772f;
にするだけで、他は変更なしで動かせる。ソースコードは以下の載せてるのでこちらを参照。
以下が動かしてみた様子。偏差の積分値に対するゲインGが小さめのためか、以前、極配置法でフィードバックゲインを計算したときよりも動きが遅い。ただ、そのぶん振子は安定している。
最適レギュレータのQ、Rを変えてゲインを計算して、挙動を観察するのもなかなか面白そうだ。次回のネタは特に決まってないので、何か思いついたらまた試してブログに書こうと思う。
参考文献
この本のMATLAB/Simulink 6か月ライセンスを使ってやってます↓
Interface 2022年 9月号
最適レギュレータや最適サーボについては以下を参考にさせて頂きましたm(_ _)m
線形 2 次レギュレーター (LQG) 設計 – MATLAB lqr – MathWorks 日本
MATLAB/Simulink記事まとめ
MATLABとSimulinkの記事は以下にまとめてます。