MATLABで最適レギュレータを設計&Unityで実装して動かしてみる
これまで極配置法によって台車型倒立振子の状態フィードバック制御を行ってきたが、今回は最適制御(最適レギュレータ)を設計して状態フィードバックをやってみる。対象はいつものように
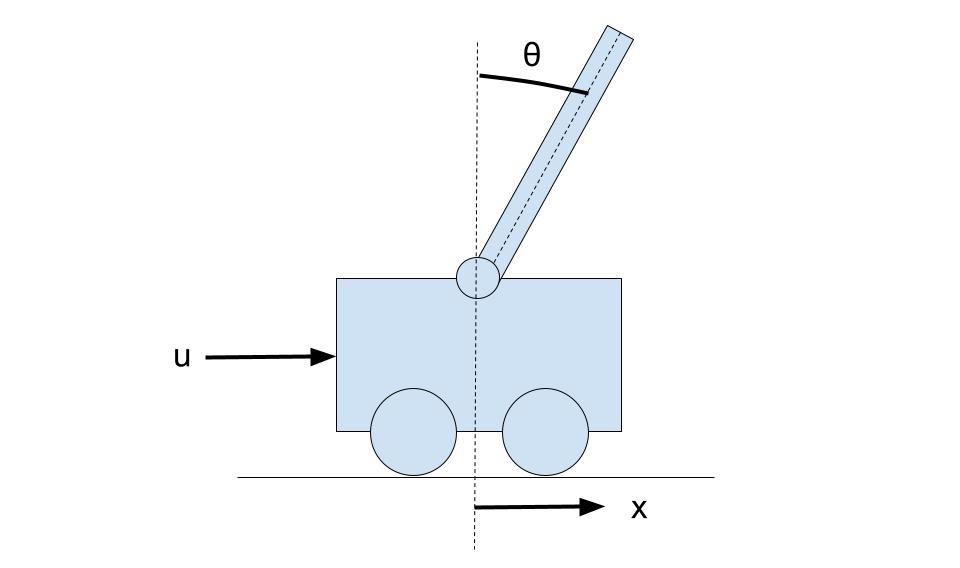
- 状態変数:台車の変位(x)、速度(dx/dt)、振子の角度(θ)、角速度(dθ/dt)
- 入力:台車に加える力(u)
として、以下の台車型倒立振子を対象とする。線形化した台車型倒立振子のモデルは以下のサイトのものをそのまま使わせて頂いているm(_ _)m
台車型倒立振子を安定にフィードバック制御する|Tajima Robotics
ちなみに最適レギュレータについては詳しく説明はしないので、参考文献などを参考にしてください。
開発環境
MATLAB online (MATLAB R2022a)
Simulink
Control System Toolbox
MATLABで最適レギュレータの設計&シミュレーション
今回は以下のようにMATLABでmファイルを実行してシミュレーションを実行した。QとRは適当に決定した。
% Parameters
M = 10;
m = 1;
L = 2;
g = 9.8;
% State Space
A = [0 1 0 0
0 0 -3*m*g/(4*M+m) 0
0 0 0 1
0 0 6*g*(M+m)/(L*(4*M+m)) 0];
B = [0
4/(4*M+m)
0
-6/(L*(4*M+m))];
C = eye(4);
D = zeros(4,1);
% Check Controllability
Co = ctrb(A,B);
rank(Co);
%Linear Quadratic Regulator
Q = diag([30 30 100 50]);
R = 1;
K = lqr(A,B,Q,R)
% Simulation
x0 = [0;
0;
0.1;
0];
sys = ss(A-B*K,B,C,D);
initial(sys,x0);
極配置法では自分で極を決めて、それに対応したフィードバックゲインKを計算したが、最適レギュレータではQ、Rを決めて評価関数を最小にするフィードバックゲインKを計算する。MATLABではlqr関数を使えばサクッと計算してくれる。今回は以下のようなゲインになった。
K = -5.4772 -16.2197 -316.3140 -114.0904
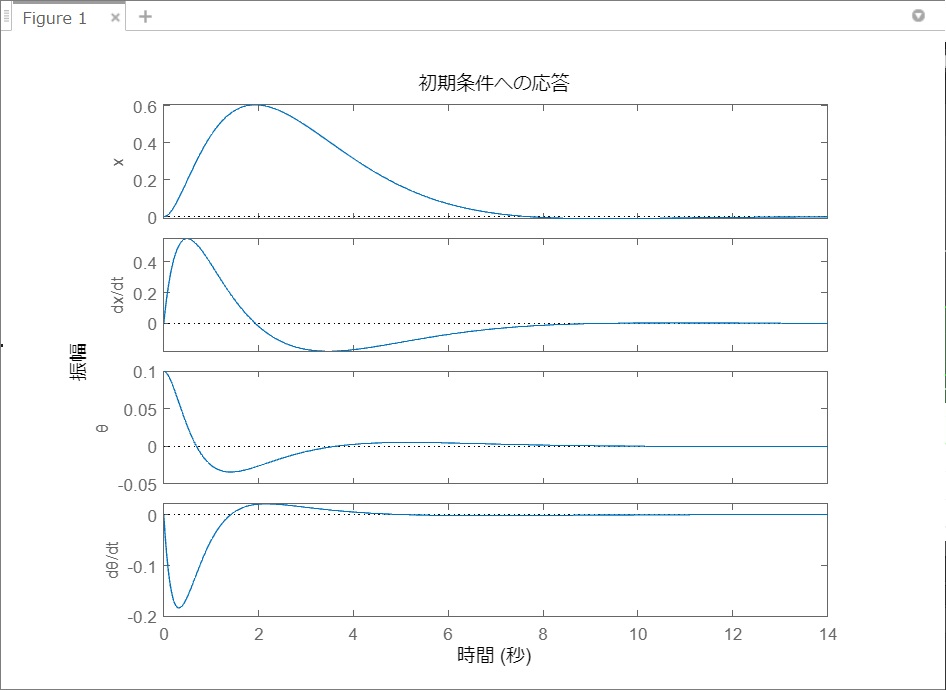
以下がinitial関数で初期状態からの応答をシミュレーションしてみた結果。θが0.1[rad]傾いた状態からスタートさせた状態からの応答になっているが、各状態変数が収束していることがわかる。
QとRは設計者が何かしらポリシーを持って(または試行錯誤的に)決める必要があるが、QとRさえ決めてしまえば状態変数、入力などを考慮した最適なフィードバックゲインが出てくるのが最適制御の便利なところ。
Unityで台車型倒立振子の動作をシミュレーションしてみる
波形だけだと味気ないので、以前のブログでやったようにUnityでも動作をシミュレーションしてみる。といっても前のMoveCart.csのソースコードのゲインを
private float k1 = -5.4772f;
private float k2 = -16.2197f;
private float k3 = -316.3140f;
private float k4 = -114.0904f;
のように変えただけで、他は変更なし。以下が動かしてみた様子。ボタンをクリックして左右から力を加えても倒立状態を維持できている。まぁゲインを変えただけなので、動画的には以前やったシミュレーションと見た目は変わらないんだけど…笑
次回は、サーボシステムを最適制御理論で設計してMATLAB/Simulinkで設計してみたいと思う。
参考文献
この本のMATLAB/Simulink 6か月ライセンスを使ってやってます↓
Interface 2022年 9月号
最適レギュレータについては以下を参考にさせて頂きましたm(_ _)m
線形 2 次レギュレーター (LQG) 設計 – MATLAB lqr – MathWorks 日本
MATLAB/Simulink記事まとめ
MATLABとSimulinkの記事は以下にまとめてます。